Research Interests
I'm Sanjukta Krishnagopal, a UC presidential postdoctoral fellow at UC Berkeley (where I am advised by Jennifer Chayes) and UCLA (where I am advised by Mason Porter). My PhD is from University of Maryland where I was advised by Michelle Girvan and was also a fellow of the CoMBiNe (Computation and Mathematics in Biological Networks) program. My research lies at the intersection of complex systems, machine learning, data science, statistics -- mainly in the development of interdisciplinary mathematical and computational methods for broad application, often in collaboration with domain scientists. My research is typically interdiscplinary, sometimes theoretical, often applied, and frequently data-driven. My research can broadly be classified into:
(1) Algorithms and models on networks: studying spectral and topological properties of higher-order graphs (e.g. hypergraphs or simplicial complexes) and multilayer networks. Inference on graphs, and dynamic networks, applied to modeling social and biological systems.
(2) Predictive medicine and multivariate time series analysis: Developing data-driven statistical and network methods for predictive and personalized medicine and gene-integrated personalized therapy in a variety of heterogeneous longitudinal diseases with complex time-evolving interactions between various different types of data.
(3) Theoretical machine learning: Deriving a theoretical understanding of neural networks in the neural tangent kernel (NTK) regime (as layer width goes to infinity). Specifically, I study properties of graph neural networks as other dimensions (size of the graphs and size of the data) go to infinity, providing theoretical guarantees for transfer learning and large graph models. I also investigate the relationship between GNNs and graph spectrum in the NTK regime.
(4) Explainable AI: Developing new machine learning architectures for explainable AI. I do this through using tools from dynamical systems to study manifold structure, and use geometric and topological properties of data to design science-aware ML algorithms. I also develop new learning rules (as alternatives to backprop) and training mechanisms for training neural networks, applied to a wide class of neural networks, including RNNs, and GNNs for faster and better learning.
(5) Mathematical models and diffusion in complex systems: studying dynamical processes on complex interacting systems. Some of my projects include: how opinions propagates in social systems - I study this through developing mathematical models that capture transitive homophily in opinion and disease spreading (which can be coupled time-evolving process). I also study the spreading of influence in political systems, to underlying the process of bill-passing in Congress. I'm particularly interested in studying how opinion propagation results in exacerbation of various types of inequalities in society, and how interventions can be adapted in a social network.
(6) Bias in society: social, algorithmic, and structural: I study how complex interactions (between more than two individuals) in higher-order coauthorship networks introduces bias (due to an individual's structural position in the higher-order network) in faculty hiring prospects and interventions to promote fair equality of opportunity (FEO). I also study, using Twitter (X) data, patterns of hate speech spreading in society for different underrepresented minorities, and ways to mitigate the effect of online hate speech on offline hate violence. Lastly, I study bias in neural networks, and ways in which they process biased or incomplete data.
(6) Cognition and computation: Understanding how learning and decision making happens in the brain through reinforcement learning and studying biologically plausible models. By studying the computational model, I hope to derive insight into brain disorders, including mental health problems and disorders that affect memory and learning.
(7) Topological Data Analysis: Topology plays an important role in studying. Here, I use existing methods in persistent homology and develop new tools that study the evolution of topological features in large data. Applications include computational chemistry, studying the evolution of language, and topological machine learning.
My CV can be found below (updated October 2023). A short description of some earlier research is found further below (updated March 2022). Please feel free to contact me for working versions of manuscripts that are not publicly available yet, if interested.
(1) Algorithms and models on networks: studying spectral and topological properties of higher-order graphs (e.g. hypergraphs or simplicial complexes) and multilayer networks. Inference on graphs, and dynamic networks, applied to modeling social and biological systems.
(2) Predictive medicine and multivariate time series analysis: Developing data-driven statistical and network methods for predictive and personalized medicine and gene-integrated personalized therapy in a variety of heterogeneous longitudinal diseases with complex time-evolving interactions between various different types of data.
(3) Theoretical machine learning: Deriving a theoretical understanding of neural networks in the neural tangent kernel (NTK) regime (as layer width goes to infinity). Specifically, I study properties of graph neural networks as other dimensions (size of the graphs and size of the data) go to infinity, providing theoretical guarantees for transfer learning and large graph models. I also investigate the relationship between GNNs and graph spectrum in the NTK regime.
(4) Explainable AI: Developing new machine learning architectures for explainable AI. I do this through using tools from dynamical systems to study manifold structure, and use geometric and topological properties of data to design science-aware ML algorithms. I also develop new learning rules (as alternatives to backprop) and training mechanisms for training neural networks, applied to a wide class of neural networks, including RNNs, and GNNs for faster and better learning.
(5) Mathematical models and diffusion in complex systems: studying dynamical processes on complex interacting systems. Some of my projects include: how opinions propagates in social systems - I study this through developing mathematical models that capture transitive homophily in opinion and disease spreading (which can be coupled time-evolving process). I also study the spreading of influence in political systems, to underlying the process of bill-passing in Congress. I'm particularly interested in studying how opinion propagation results in exacerbation of various types of inequalities in society, and how interventions can be adapted in a social network.
(6) Bias in society: social, algorithmic, and structural: I study how complex interactions (between more than two individuals) in higher-order coauthorship networks introduces bias (due to an individual's structural position in the higher-order network) in faculty hiring prospects and interventions to promote fair equality of opportunity (FEO). I also study, using Twitter (X) data, patterns of hate speech spreading in society for different underrepresented minorities, and ways to mitigate the effect of online hate speech on offline hate violence. Lastly, I study bias in neural networks, and ways in which they process biased or incomplete data.
(6) Cognition and computation: Understanding how learning and decision making happens in the brain through reinforcement learning and studying biologically plausible models. By studying the computational model, I hope to derive insight into brain disorders, including mental health problems and disorders that affect memory and learning.
(7) Topological Data Analysis: Topology plays an important role in studying. Here, I use existing methods in persistent homology and develop new tools that study the evolution of topological features in large data. Applications include computational chemistry, studying the evolution of language, and topological machine learning.
My CV can be found below (updated October 2023). A short description of some earlier research is found further below (updated March 2022). Please feel free to contact me for working versions of manuscripts that are not publicly available yet, if interested.
Current Position: UC Presidential Postdoc
|
| ||||||
Primary Research Themes
Machine Learning
A biologically plausible alternative to backpropagation for learning
How does learning occur? How do weights change? Machine learning's answer to this is backpropagation, however this is not biologically plausible, and networks trained with this rule tend to forget old tasks when learning new ones. We propose a novel learning rule as an alternative to backpropagation, that involves local learning rules only (each layer computes it's own error without backpropagating). Naively, this will likely not work, as it removes the effectiveness of multiple layers, however, we use a gating mechanism that segregates the weights based on input. i.e., if two inputs are close to each other, the set of weights that change have large overlap, and if two inputs are far away, then the set of weights that learn them have very little to no overlap. Dendritic Gated Networks are significantly more data efficient than conventional artificial networks and are highly resistant to forgetting, and we show that they perform well on a variety of tasks, in some cases better than backpropagation. The DGN bears similarities to the cerebellum and validates some experimental results from in vivo mouse cerebellar imaging.
I gave a talk on this work at Cosyne 2021 which had an audience of 1200 people! (and a 5% acceptance rate). This work is done in collaboration with Google Deepmind
Arxiv paper
I gave a talk on this work at Cosyne 2021 which had an audience of 1200 people! (and a 5% acceptance rate). This work is done in collaboration with Google Deepmind
Arxiv paper
ENCODED PRIOR SLICED WASSERSTEIN AUTOENCODER: LEARNING LATENT MANIFOLD REPRESENTATIONS
I am interested in learning latent representations of which preserve the geometry and topology of the data. In a sense, embedding the entire data manifold. Naturally, this should vastly improve interpretability of latent space, and interpolation in it. In VAEs the use of conventional priors can limit their ability to encode the underlying structure of data.
here we introduce EPSWAE, where the latent representation is learned through a different network preserves the topological and geometric properties of the data manifold. The use of the Wasserstein distance (as opposed to the KL divergence) makes this possible.
A second interest of mine is navigating and interpreting the latent space. If the latent space lies on a low-d manifold, it's natural to interpolate along geodesics such that intermediate points lie on the manifold. I propose a network-geodesics algorithm to do exactly that, as opposed to conventional linear interpolation in latent space.
Arxiv link
here we introduce EPSWAE, where the latent representation is learned through a different network preserves the topological and geometric properties of the data manifold. The use of the Wasserstein distance (as opposed to the KL divergence) makes this possible.
A second interest of mine is navigating and interpreting the latent space. If the latent space lies on a low-d manifold, it's natural to interpolate along geodesics such that intermediate points lie on the manifold. I propose a network-geodesics algorithm to do exactly that, as opposed to conventional linear interpolation in latent space.
Arxiv link
interpretable learning: Reservoir computing
|
Reservoir computing is a machine learning architecture that is a popular model for foundational study of neural network dynamics - since the reservoir itself is a dynamical system. The connections between the neurons are recurrent, and follow a differential equation that can be solved (numerically) to reveal interesting dynamical states/attractors. Thus the learning is encoded in the dynamical state of the reservoir computer in response to the input, which is a radically different way of thinking of about learning. This property of reservoir computers makes them an ideal candidate for understanding how learning occurs, i.e., not a black box, and learn chaotic models (hence, widely popular in modeling weather patterns). A bonus is that they can be implemented in hardware!
My research in reservoir computing spans a variety of topics that have resulted in three publications: Generalization of learning using very little data, Understanding how learning occurs through attractors in the reservoir dynamics, Separating chaotic signals e.g. a chaotic version of the cocktail party problem. |
|
graph neural networks: spectral analysis for improved features
Graph neural networks do many wonderful things with graphical data structures, but are still somewhat of a black box. I am interesting in understanding how the spectrum of the graph laplacian can be harnessed to improve learning in the GNN framework. There are many directions one may explore in this direction, one in particular that I am interested in is exploring the graph neural tangent kernel limit (wide limit), where there exist theoretical guarantees of a convex loss function. I am interested in understanding how growing a graph along directions that maximize eigenvalues may be related to the selection of features, and speed of convergence.
I also use graph neural networks in application such as predictive medicine. See this paper.
I also use graph neural networks in application such as predictive medicine. See this paper.
Topological Data analysis and machine learning for materials
Here I attempt to use computational tools to predict properties of compounds called metal-organic-frameworks (MOFs). These materials are incredibly useful in gas purification (like removing CO2 from the environment), gas storage (like storing ultracold gases), and even as superconductors. They naturally are incredibly useful in climate change related applications, however are difficult and time consuming to synthesize. By using machine learning and topological data analysis, I attempt to study the structures of existing MOFs, to predict which new ones (new combinations of metals and organic components) will have useful properties. This is ongoing joint work with Jennifer Chayes, Christian Borgs, and Aditi Krishnapriyan.
Network and data science
Computational biology: personalized medicine and genomics
|
This theme of research involves computational methods for medical application. This involves applying various techniques from multilayer networks, graph neural networks and statistics to predict disease subtypes in patients early on, and consequently pre-emptively treat them. In particular, I developed the 'Trajectory Clustering' algorithm that identifies disease subtypes in heterogenous multivariate diseases, where conventional methods face two main challenges challenges (1) unable to capture time-evolution of interactions, (2) can't handle multiple types of data (ordinal, categorical, continuous, phenotypic and genetic etc.). I collaborate with several clinicians on Parkinson's and Stroke. Three papers have resulted from this theme
Publications: Plos One paper. Biomedical Physics and Engineering Express paper. Stroke paper. and Talk at NetSci 2018, Paris here |
Higher order networks: simplicial complexes
|
While graphs are a source of rich information about pairwise interactions, several real world networks involve interactions between more than two agents. For example three students meeting in a break room is a simultaneous 3-way interaction (represented by a filled traingle), not 3 pairwise interactions. So many real networks are higher-order, and often misleadingly reduced to pairwise interactions. Simplicial complexes are powerful tools to model higher order interactions. The nice thing about them is that they have mathematical definitions and can be analyzed through the lens of topology and geometry. I am interested in developing a theoretical understanding of higher-order networks, particularly properties of the higher order (Hodge) Laplacian. I am also interested in various applications.
My most recent investigation involves spectral community detection in an arbitrary dimensional simplicial complex (any number of interacting nodes). I am also studying concepts such as 'holes' or cavities in higher order networks. Manuscript: Sanjukta Krishnagopal and Ginestra Bianconi |
The cooperative vs competitive dynamics in extreme mountaineering
I enjoy hiking, and am deeply fascinated by extreme mountaineering, even though I haven't actually brought myself to do anything too dangerous. I decided, as a pet data analysis project, to study the various factors both personal and expeditional (and their interactions) that contribute to success/ various types of failure at extremely high altitudes in the Everest ranges. These factors include oxygen use, age, sex, previous expedition etc. but also length of expedition, ratio of sherpas to paying climbers, number of high camps. This necessitated the use of a multiscale network and regression. This topic and the results are personally exciting! I will be presenting this work at Complex Networks 2021 in Madrid. Check out my two recent papers: this and that .
social dynamics coupled with disease spreading - segregation in society
Social relationships evolve constantly, changing patterns of interactions between individuals. Humans are known to be homophilic, i.e., we like to befriend people that are similar to ourselves. Hence, the social network of individuals changes with time, based on how the opinions of people around them align with their own. Conversely, individuals change their opinions, through interactions with others in their network. Lastly, the evolution of these relationships affects the ways in which contagious diseases spread. In this ongoing work, I develop models of opinion-dynamics coupled with disease spreading processes. I investigate how and when consensus or fragmentation occurs within societies, and attempt to capture the fickle nature of relationships through a changing social network. I attempt to do this through computationally modeling, mathematical support, and topological data analysis. I am particularly interested in understanding how mechanisms of human behavior lead to fragmentation of society and inequalities such as differential healthcare, school systems, economic opportunities etc. My interest is to propose policy interventions that mitigate social inequalities.
Selected Past Research Projects
generalized similarity learning with limited data
|
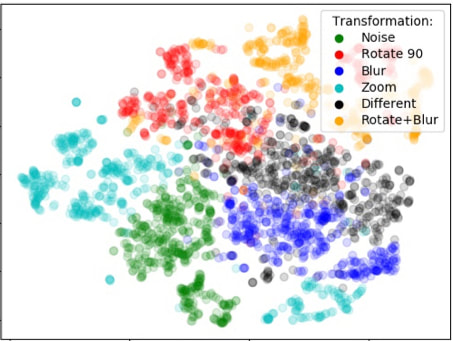
We investigate the ways in which a machine learning architecture known as Reservoir Computing that loosely resembles neural dynamics learns concepts such as “similar” and “different” and other relationships between image pairs and generalizes these concepts to previously unseen classes of data. We find that the reservoir acts as a nonlinear filter that projects the input into the high dimensional reservoir space, where inputs from the same category cluster together (see figure), allowing for easy generalization to unseen data. Our architecture outperforms conventional pair-based methods such as Siamese Neural Networks.
Advised by Yiannis Aloimonos and Michelle Girvan Published in Complexity. Manuscript here |
Synchorinzation patterns in fractal networks: from structure to function
|
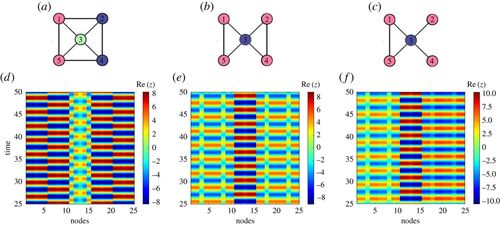
We investigate complex synchronization patterns such as cluster synchronization and partial amplitude death in networks of coupled Stuart–Landau oscillators with fractal (hierarchical) connectivities. The study of fractal or self-similar topology is motivated by the network of neurons in the brain. Our results show that there is a direct correlation between topology and dynamics (see top figure) - hierarchical networks display hierarchical dynamics.
Advised by Prof. Eckehard Schoell, PhD Published in Philosophical Transactions of the Royal Society. Manuscript here |
Steganography and double key protection using chaotic maps
|
We developed the image encryption algorithm based on the chaotic logistic map and cat map. A secret key is used to determine initial conditions and the input to the chaotic map function. The Lorenz map is then used for successive pixel encryption. To make the cipher more robust against any attack, the secret key is modified after encrypting each pixel of the image using Arnold’s cat map. Decryption follows the exact reverse. Figures on the right show original (top), encrypted (middle) and recovered after decryption (bottom) with minimal loss. The encrypted image is then hidden using a steganography technique that uses a cover image along with the Lorenz map to determine the location of the pixels to be hidden in the cover. Tests on efficiency and key sensitivity show that our double-key method provides secure image encryption and real-time transmission.
Advised by Dr. Bijil Prakash Published in Proceedings of Fourth International Conference on Soft Computing, 2014 Manuscript here |
Wasserstein autoencoder to learn latent representation of data manifold
|
Variational autoencoders have been very successful generative models for a variety of tasks, but the use of conventional Gaussian or Gaussian mixture priors are limited in their ability to capture topological or geometric properties of data in the latent representation. Here we introduce a new architecture that learns the prior, showing that our model can encode topological properties of the data in the latent space. We use this to generate improved interpolations along the data manifold with image data.
|
Biconvlstm for violence detection in videos
|
We introduce a Bidirectional Convolutional LSTM architecture for violence detection. The encoding of temporal features in both directions allows for a better video representation. Our method performs comparably with state of the art architectures on benchmarked datasets.
Conference proceedings, Workshop for Objectionable Content and Misinformation at ECCV 2018. Publication here |
Encoding of chaotic dynamics in the weights of a recurrent neural network
We study the dynamical properties of a machine learning model called Reservoir Computing (RC) using a novel mathematical tool called 'directional fiber' in order to gain insight into how information is encoded through learning. The RC is trained to predict the chaotic Lorenz signal - chaotic signals are just that, mathematically chaotic, and hence extremely hard to predict. We find that the reservoir, which is a dynamical system itself, after training, emulates properties of the system it is trained on, i.e., contains a higher dimensional projection of the Lorenz fixed points.
IJCNN 2019 paper
IJCNN 2019 paper
For questions and code please contact me
Link to my github
Link to my github
Chimeraki
Copyright 2018
Copyright 2018